Рынок облигаций. Анализ и стратегии

Фрэнк Дж. Фабоцци, 2007

Фрэнк Фабоцци – специалист мирового масштаба в области облигаций. Его книги – основной источник информации для финансовых специалистов, которые изучают облигации. По ним учат в ведущих бизнес-школах и сдают экзамены на CFA (Chartered Financial Analyst). Эта книга – прекрасный учебник для любого финансиста. Из нее читатель узнает о: фундаментальных характеристиках облигаций; типах эмитентов; сроках погашения облигаций и их значимости; ценных бумагах с фиксированной и плавающей ставкой; облигациях со встроенными опционами и влиянии встроенных опционов на денежный поток облигаций; типах встроенных опционов; конвертируемых облигациях; видах рисков инвестора в ценные бумаги с фиксированным доходом; некоторых способах классификации финансовых инноваций; инструментах управления портфелем облигаций и многом другом. Во второе издание добавлены главы, касающиеся моделирования процентных ставок и кредитного риска, а также кредитного анализа корпоративных облигаций. Книга рассчитана на сотрудников финансовых компаний и банков, инвесторов, а также студентов и преподавателей экономических вузов. В формате epub сохранен издательский макет.

Глава 2. ЦЕНООБРАЗОВАНИЕ ОБЛИГАЦИЙ

В этой главе читателю будут представлены сведения:

• о временно́й стоимости денег;

• о способах вычисления цены облигации;

• о том, что для установления цены облигации необходимо определить размер предполагаемых денежных потоков и величину доходности, с помощью которой должны быть дисконтированы предполагаемые денежные потоки;

• о том, почему цена облигации меняется в направлении, противоположном изменению требуемой доходности;

• о выпуклой кривой, выражающей соотношение между ценой и доходностью безопционной облигации;

• о взаимосвязи купонной ставки, требуемой доходности и цены;

• об изменении цены облигации по мере приближения к дате погашения;

• о причинах изменения цены облигации;

• о сложностях, связанных с ценообразованием облигаций;

• о ценообразовании облигаций с плавающей купонной ставкой и с обратной плавающей купонной ставкой;

• о понятии накопленного купонного дохода и котировках цен на облигации.

В этой главе мы объясняем механизм ценообразования облигаций, в следующей — описываем способы измерения доходности. Понимание моделей ценообразования, а также мер доходности невозможно без уяснения основополагающего принципа функционирования финансового рынка, а именно — временно́й стоимости денег. Мы, таким образом, начинаем главу с объяснения этого базового положения.

ВРЕМЕННАЯ СТОИМОСТЬ ДЕНЕГ

Понятие временно́й стоимости денег — важнейший принцип, лежащий в основе анализа любого финансового инструмента. Деньги обладают временно́й стоимостью, поскольку могут быть инвестированы на некий срок под некий процент.

Будущая стоимость

Определить будущую стоимость любой суммы денег, инвестированной в настоящий момент, можно по формуле:

P_n = P₀(1 + r)ⁿ, (2.1)

где:

n — число периодов;

P_n — будущая стоимость через n периодов, считая с настоящего момента (в долларах);

P₀ — номинальная стоимость (в долларах);

r — процентная ставка на один период (в десятичных дробях).

Выражение (1 + r)ⁿ представляет будущую стоимость одного доллара, инвестированного в настоящий момент на n периодов под процентную ставку r.

Предположим, что менеджер пенсионного фонда инвестирует $10 млн в финансовый инструмент, который в течение шести лет должен приносить 9,2 % ежегодно. Будущая стоимость $10 млн будет равна $16 956 500, поскольку:

P₆ = $10 000 000 × 1,092⁶ = $10 000 000 × 1,69565 = $16 956 500.

Из приведенного примера видно, как подсчитывать будущую стоимость в случае, когда процент выплачивается один раз в год (т. е. величина периода равна числу лет). Если процент выплачивается чаще, чем раз в год, то как величина процентной ставки, так и число периодов, используемых для расчета будущей стоимости, должны быть уточнены следующим образом:

Допустим, что портфельный менеджер из первого примера инвестирует свои $10 млн в финансовый инструмент, который в течение шести лет должен приносить 9,2 % ежегодно, однако процентные выплаты осуществляются раз в шесть месяцев (т. е. дважды в год). В этом случае:

и

P₁₂ = $10 000 000 × 1,046¹² = $10 000 000 × 1,71546 = $17 154 600.

Обратите внимание на то, что будущая стоимость $10 млн в ситуации, когда процент выплачивается раз в полгода ($17 154 600), больше, чем в случае процентных выплат раз в год ($16 956 500), несмотря на то что обе инвестиции осуществляются под один и тот же годовой процент. Более высокая будущая стоимость суммы, вложенной под процент, выплачиваемый раз в полгода, отражает более выгодные возможности реинвестирования получаемых процентных платежей.

Будущая стоимость обычного аннуитета

Периодически инвестируемая неизменная сумма денег носит название аннуитета. Если первая инвестиция осуществляется через один период, считая от настоящего момента, принято говорить об обычном аннуитете. Будущая стоимость обычного аннуитета может быть найдена путем вычисления будущей стоимости каждой из инвестиций в момент окончания инвестиционного горизонта, а затем сложения полученных будущих стоимостей. Будущую стоимость обычного аннуитета легче, однако, рассчитать по формуле:

(2.2)

где А — размер аннуитета (в долларах). Выражение в скобках — это будущая стоимость обычного аннуитета, равного $1, на момент окончания n периодов.

Применение формулы хорошо иллюстрирует следующий пример: допустим, что портфельный менеджер приобретает облигации номинальной стоимостью $20 млн, которые в течение 15 лет должны приносить 10 % годовых. Эмитент осуществляет купонные выплаты раз в год, первый платеж будет совершен через год. Сколько получит портфельный менеджер при условии, что он: 1) останется держателем облигации до даты погашения, т. е. все 15 лет, и 2) будет инвестировать ежегодные купонные выплаты под годовую ставку 8 %?

Через 15 лет портфельный менеджер станет обладателем:

1) $20 млн в момент погашения облигации;

2) 15 ежегодных купонных выплат по $2 млн каждая (0,10 × $20 млн);

3) процента, полученного от инвестирования ежегодных купонных выплат под 8 % годовых.

Сумму пунктов 2 и 3 можно вычислить, применив формулу (2.2). В нашем примере аннуитет составляет $2 000 000 в год. Таким образом:

A = $2 000 000; r = 0,08; n = 15

и

Будущая стоимость обычного аннуитета, равного $2 000 000 в год, в течение 15 лет инвестируемого под 8 %, составляет $54 304 250. Поскольку $30 000 000 (15 × $2 000 000) этой будущей стоимости представляют собой ежегодные купонные выплаты (в долларах), осуществляемые эмитентом и инвестируемые портфельным менеджером, баланс в размере $24 304 250 ($54 304 250 — $30 000 000) — это процент, полученный от реинвестирования данных ежегодных купонных выплат. Таким образом, общая сумма (в долларах), которую портфельный менеджер получит через 15 лет от совершенных инвестиций, окажется равна:

В главе 3 мы объясним, почему для определения относительной стоимости облигаций необходимо совершать подсчет общей будущей суммы в долларах на момент окончания установленного портфельным менеджером инвестиционного горизонта.

Давайте снова проведем анализ данной облигации, предположив на этот раз, что при той же годовой ставке купонные выплаты осуществляются раз в шесть месяцев; первая выплата произойдет через полгода и будет немедленно реинвестирована. Допустим, что получаемые раз в полгода купонные выплаты могут быть реинвестированы под 8 % годовых.

Купонные выплаты, получаемые раз в полгода, составляют $1 000 000 каждая. Будущая стоимость 30 полугодовых купонных выплат по $1 000 000 плюс процент, получаемый от инвестирования купонных выплат, подсчитывается следующим образом:

Поскольку купонные выплаты составляют $30 000 000, процент, получаемый от реинвестирования купонных выплат равен $26 085 000. Возможность более часто совершать реинвестирование купонных выплат — причина того, что полученная от реинвестиций сумма ($26 085 000) оказалась больше, чем сумма ($24 304 250), принесенная реинвестированием купонных выплат, осуществляемых раз в год.

Таким образом, общая сумма (в долларах), которую портфельный менеджер получит через 15 лет от предпринятого инвестирования, окажется равна:

Приведенная стоимость

Мы показали, как можно вычислить будущую стоимость инвестиций. Объясним теперь обратный процесс, а именно: как определить количество денег, которые надо вложить сегодня для получения определенной стоимости в будущем. Такая сумма денег получила название приведенной стоимости. Поскольку, как будет сказано далее в этой главе, цена любого финансового инструмента — это приведенная стоимость его предполагаемого денежного потока, понятие приведенной стоимости необходимо уяснить всякому инвестору, желающему разобраться в механизме ценообразования инструментов с фиксированным доходом.

Итак, мы хотим узнать, каким образом определить размер денежной суммы, которую надо инвестировать сегодня под процент r, выплачиваемый раз в период в течение n периодов, чтобы получить заданную будущую стоимость. Формула вычисления может быть получена из формулы (2.1), предназначенной для подсчета будущей стоимости инвестиции (Р₀):

Заменим Р₀ на приведенную стоимость (PV):

Выражение в скобках — это приведенная стоимость одного доллара. Оно показывает, сколько должно быть вложено сегодня, для того чтобы через n периодов получить $1 при условии существования процентных ставок, равных r, в течение каждого периода.

Процесс вычисления приведенной стоимости носит название дисконтирования. Приведенная стоимость, таким образом, иногда называется дисконтированной стоимостью, а процентные ставки — дисконтными ставками.

Продемонстрируем действие формулы (2.3) на конкретном примере. Допустим, что портфельный менеджер может приобрести финансовый инструмент, который через семь лет принесет $5 млн при отсутствии промежуточных денежных потоков. Портфельный менеджер хочет получать на свои инвестиции 10 % годовых. Приведенная стоимость инвестиций должна быть подсчитана как:

Оказывается, что инвестирование в настоящий момент суммы $2 565 791 под 10 % годовых через семь лет принесет $5 млн. Допустим, что данный финансовый инструмент продается дороже, чем за $2 565 791. Это значит, что, купив его по цене, превышающей $2 565 791, портфельный менеджер получит от своих инвестиций меньше, чем 10 % годовых. И наоборот: если финансовый инструмент продается дешевле, чем за $2 565 791, портфельный менеджер получит от своих инвестиций больше, чем 10 % годовых.

Существуют два основных свойства приведенной стоимости, которые читатель должен себе уяснить. Во-первых, для данной будущей стоимости в установленный момент времени в будущем, чем выше процентные (или дисконтные) ставки, тем ниже приведенная стоимость. Причина падения приведенной стоимости с ростом процентных ставок легко объяснима: чем больше процентные ставки, под которые совершаются в настоящий момент инвестиции, тем меньшая сумма денег должна быть вложена, чтобы получить заданную будущую стоимость.

Второе свойство приведенной стоимости: при данных процентных (дисконтных) ставках, чем длиннее временной горизонт, по окончании которого должна быть получена будущая стоимость, тем ниже приведенная стоимость. Описанный эффект объясняется следующим образом: на более продолжительном отрезке времени успевает накопиться бо́льшая сумма процентных выплат. Таким образом, начальная инвестируемая сумма может быть меньше.

Приведенная стоимость серии будущих стоимостей

В большинстве встречающихся в ходе управления портфелем ситуаций финансовый инструмент генерирует серию будущих стоимостей. Определить приведенную стоимость серии будущих стоимостей можно, если подсчитать сначала приведенную стоимость каждой из будущих стоимостей. Затем, для вычисления приведенной стоимости всей серии в целом, следует сложить полученные значения будущих стоимостей.

Формула в этом случае будет выглядеть так:

Предположим, например, что портфельный менеджер собирается купить финансовый инструмент, от которого следует ожидать следующих выплат:

Допустим, что портфельный менеджер хотел бы инвестировать под 6,25 % годовых. Приведенная стоимость данной инвестиции может быть вычислена следующим образом:

Приведенная стоимость обычного аннуитета

Неизменная сумма денег (в долларах), получаемая через равные промежутки времени или выплачиваемая раз в год, называется аннуитетом. Если первую выплату инвестор получает через один период, считая с настоящего момента, аннуитет называется обычным. Существует также форма немедленной выплаты, которую, однако, мы не будем здесь рассматривать — в данной книге речь пойдет только об обычном аннуитете.

Вычисление приведенной стоимости обычного аннуитета производится следующим образом: сначала подсчитываются приведенные стоимости каждой из будущих стоимостей, затем все полученные значения суммируются. Возможно также использование следующей формулы:

где А — размер аннуитета (в долларах). Выражение в скобках — это приведенная стоимость обычного аннуитета, равного $1, для n периодов.

Предположим, что от своих инвестиций инвестор в течение восьми лет рассчитывает получать по $100 в конце каждого года; дисконтная ставка, используемая для дисконтирования, равна 9 %. Приведенная стоимость такого обычного аннуитета составит:

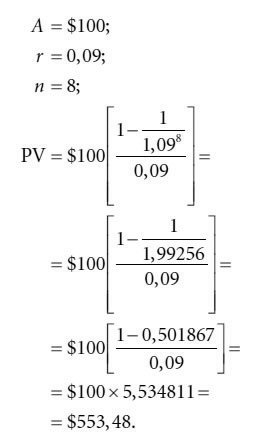
Приведенная стоимость в случае выплат, производимых чаще одного раза в год

Вычисляя приведенную стоимость, мы предполагали, что будущая стоимость будет выплачена или получена раз в год. В реальной практике, между тем, будущую стоимость инвестор может получать чаще, чем раз в год. В подобной ситуации формулу, принятую нами для установления значения приведенной стоимости, следует уточнить. Во-первых, годовая процентная ставка делится на количество выплат в год. (В действительности такой метод уточнения величины процентной ставки не является корректным. Научно обоснованный метод уточнения данного значения приводится в главе 3.) Так, если будущие стоимости выплачиваются раз в полгода, годовая процентная ставка делится на 2; если они выплачиваются раз в квартал, годовую процентную ставку следует делить на 4. Во-вторых, число периодов, в течение которых инвестор будет получать будущую стоимость, должно быть уточнено путем умножения числа лет на количество выплат в год.

ЦЕНООБРАЗОВАНИЕ ОБЛИГАЦИИ

Цена любого финансового инструмента равна приведенной стоимости предполагаемого денежного потока от данного финансового инструмента. Таким образом, для определения цены следует знать:

1) размер предполагаемых денежных потоков;

2) величину подходящей требуемой доходности (требуемой ставки).

Предполагаемые денежные потоки для одних финансовых инструментов вычисляются легко, для других — с большей сложностью. Требуемая доходность — это величина, отражающая доходность финансовых инструментов со сравнимым риском, иными словами — доходность альтернативных инвестиций.

Первый шаг, который мы делаем, приступая к определению цены облигации, — определение ее денежных потоков. Денежные потоки от облигации, которую эмитент не имеет права погасить до установленной даты погашения (т. е. облигация без встроенного колл-опциона)^[7], состоят из:

1) периодических купонных выплат, осуществляемых вплоть до даты погашения;

2) номинальной стоимости (стоимости погашения), получаемой в момент погашения облигации.

Для упрощения анализа механизма ценообразования облигаций, договоримся считать действительными три утверждения:

1. Купонные выплаты осуществляются раз в полгода (по большинству американских облигаций купон действительно выплачивается раз в шесть месяцев).

2. Ближайшая выплата купона состоится ровно через шесть месяцев.

3. Купонная ставка фиксирована на весь срок до погашения облигации.

Итак, денежный поток облигации без встроенного колл-опциона состоит из аннуитета фиксированных купонных выплат, получаемых раз в полгода, и номинальной стоимости. 20-летняя облигация с купонной ставкой 10 % и номиналом $1000 от купонных выплат получит следующий денежный поток:

купонная выплата за год = $1 000 × 0,10 = $100;

купонная выплата за полгода = $100/2 = $50.

Таким образом, существует 40 денежных потоков по $50, получаемых каждые полгода, и денежный поток, равный $1000, который будет получен через 40 полугодовых периодов. Обратите внимание на описание номинальной стоимости. Мы не говорим, что получим ее через 20 лет — номинал описывается в тех же терминах, что и купон, выплачиваемый раз в шесть месяцев.

Требуемая доходность выясняется после изучения рыночных доходностей облигаций, сравнимых с нашей. Под сравнимыми понимаются облигации без встроенного колл-опциона, имеющие то же кредитное качество и тот же срок до погашения^[8].

Требуемая доходность, как правило, выражается в процентах годовых. В ситуации, когда денежные потоки поступают раз в полгода, в качестве процентной ставки для дисконтирования денежных потоков принято использовать половину годовой процентной ставки.

Размеры денежных потоков и требуемая доходность — аналитические данные, достаточные для вычисления цены облигации. Поскольку ценой облигации является приведенная стоимость денежных потоков, ее значение вычисляется путем сложения следующих двух величин:

1) приведенной стоимости полугодовых купонных выплат;

2) приведенной стоимости номинала в момент погашения.

В общих чертах формула подсчета цены выглядит следующим образом:

где:

P — цена (в долларах);

n — число периодов до погашения (число лет, умноженное на 2);

C — полугодовая купонная выплата (в долларах);

r — процентная ставка, соответствующая периоду (требуемая годовая доходность, деленная на 2);

M — стоимость номинала;

t — количество периодов, оставшихся до получения платежа.

Полугодовые выплаты купона представляют собой обычный аннуитет, поэтому, используя формулу (2.5) для вычисления приведенной стоимости обычного аннуитета, получаем приведенную стоимость купонной выплаты, равную:

Для того чтобы читатель понял, как на практике осуществляется вычисление цены облигации, рассмотрим 20-летнюю облигацию с купоном, равным 10 %, и номинальной стоимостью $1000. Допустим, что требуемая доходность для этой облигации составляет 11 %. Данная облигация приносит следующие денежные потоки:

1) 40 полугодовых купонных выплат по $50 каждая;

2) $1000 через 40 полугодовых периодов.

Полугодовая (соответствующая периоду) процентная ставка (или соответствующая периоду требуемая доходность) равна 5,5 % (11 % поделить на 2).

Приведенная стоимость 40 полугодовых купонных выплат по $50, дисконтированная по 5,5 %, согласно результатам приведенных ниже вычислений, составляет $802,31:

Приведенная стоимость номинала в $1000, который будет получен через 40 полугодовых периодов, дисконтированная по 5,5 %, равна, как видно из расчетов, приведенных ниже, $117,46:

Цена облигации, таким образом, равна сумме двух приведенных стоимостей:

Предположим теперь, что требуемая доходность составляет не 11 %, а 6,8 %. Цена облигации в этом случае окажется равной $1347,04 (процесс вычисления значения цены описан ниже).

Приведенная стоимость купонных выплат при соответствующей периоду процентной ставке 3,4 % (6,8 % /2) равна:

Приведенная стоимость номинала в $1000, который будет получен через 40 полугодовых периодов, дисконтированная по 3,4 %, равна:

Цена облигации, таким образом, составит:

Если требуемая доходность равна купонной ставке 10 %, цена облигации будет равна ее номинальной стоимости, т. е. $1000. Действительно, приведенная стоимость купонных выплат при соответствующей периоду процентной ставке 5 % (10 %/2) равна:

Приведенная стоимость номинала в $1000, который будет получен через 40 полугодовых периодов, дисконтированная по 5 %, равна, согласно формуле:

Цена облигации, таким образом, составит:

Ценообразование облигаций с нулевым купоном

Некоторые облигации не предполагают никаких периодических купонных выплат. Инвестор получает процентный доход за счет разницы между номинальной стоимостью и ценой покупки. Облигации этого типа носят название облигаций с нулевым купоном. Цена облигации с нулевым купоном вычисляется путем подстановки нуля вместо С в формулу (2.6):

Формула (2.8) показывает, что цена облигации с нулевым купоном — это приведенная стоимость номинала. Заметим, однако, что при подсчетах такой приведенной стоимости число периодов, используемое для дисконтирования, равно не количеству лет до погашения облигации, а количеству лет, умноженному на 2. Дисконтная ставка в этом случае равна половине требуемой годовой доходности. Так, цена облигации с нулевым купоном и сроком до погашения 15 лет, номинал которой равен $1000, а требуемая доходность — 9,4 %, составит $252,12:

Связь цены и доходности

Одно из фундаментальных свойств облигации заключается в том, что цена всегда меняется в направлении, противоположном изменению требуемой доходности. Объяснение этому феномену следует искать в том факте, что цена облигации — это приведенная стоимость денежных потоков. Если требуемая доходность увеличивается, то приведенная стоимость денежных потоков падает; соответственно, падает и цена. И наоборот: падение требуемой доходности означает рост приведенной стоимости денежных потоков, а значит, и рост цены. Проверим справедливость этого утверждения на примере цены 20-летней 10 %-ной облигации в случаях, когда требуемая доходность составляет 11 %, 10 % и 6,8 %. В табл. 2.1 приводятся цены 20-летней облигации с 10 %-ным купоном при разных требуемых доходностях.

Таблица 2.1. Связь цены и доходности для 20-летней облигации с 10 %-ным купоном

Изобразив связь цены и доходности любой облигации без встроенного колл-опциона графически, мы обнаружим, что график имеет характерную изогнутую форму, показанную на рис. 2.1.

Кривая такой формы носит название выпуклой. Выпуклость кривой цена/доходность имеет важное значение при оценке инвестиционных характеристик облигации (подробнее об этом сообщается в главе 4).

Связь между купонной ставкой, требуемой доходностью и ценой

Рыночным доходностям свойственно меняться; единственная переменная, которая меняется, чтобы соответствовать новой требуемой доходности, — это цена облигации. Если купонная ставка равна требуемой доходности, цена акции будет равна ее номиналу — мы показали это на примере 20-летней облигации с купонной ставкой в 10 %.

Как только в данный момент времени рыночная доходность поднимается выше купонной ставки, цена облигации приспосабливается к новым условиям таким образом, чтобы инвестор, приобретающий облигацию, мог получить от покупки некую дополнительную выгоду. Если бы цена не менялась, инвесторы отказались бы от приобретения облигации, предлагающей доходность ниже рыночной. Таким образом, недостаток спроса приводит к падению цены и росту доходности облигации. Именно так на практике происходит падение цены ниже уровня номинала.

Прирост капитала, реализуемый путем удерживания облигации до даты погашения, — форма компенсации, предлагаемой инвестору, владеющему облигацией с купонной ставкой ниже требуемой доходности. Если облигация продается по цене более низкой, чем ее номинальная стоимость, говорят, что облигация была продана с дисконтом. Из приведенных выше расчетов видно, что в ситуации, когда требуемая доходность превышает купонные ставки, цена облигации всегда ниже номинала ($1000).

Если требуемая рыночная доходность меньше купонной ставки, облигация должна продаваться по цене более высокой, чем номинальная стоимость. Это происходит потому, что инвестор, приобрети он облигацию по номиналу, получил бы купонную ставку, превышающую справедливую рыночную доходность. В результате цена на облигацию со столь привлекательной доходностью пошла бы вверх. Цена может расти до тех пор, пока доходность облигации не совпадет с требуемой доходностью рынка. Про облигацию, цена которой превышает ее номинальную стоимость, говорят, что она продается с премией. Отношения между купонной ставкой, требуемой доходностью и ценой в общем виде можно записать следующим образом:

купонная ставка < требуемая доходность ↔ цена < номинал (облигация торгуется с дисконтом)

купонная ставка = требуемая доходность ↔ цена = номинал

купонная ставка > требуемая доходность ↔ цена > номинал (облигация с торгуется премией).

Связь между ценой облигации и временем при неизменных процентных ставках

Что происходит с ценой облигации, если в течение периода между приобретением облигации и датой погашения требуемая доходность не меняется? Для облигации, продающейся по номиналу, купонная ставка равна требуемой доходности. Дата погашения будет приближаться, но облигация по-прежнему будет продаваться по номинальной стоимости. Ее цена по мере приближения к дате погашения не изменится.

Цена облигации не останется прежней в случае, если облигация продается с дисконтом или с премией. В табл. 2.2 приведены данные о временно́м движении цены 20-летней облигации с купонной ставкой 10 %, продающейся с дисконтом, а также данные о той же самой облигации, продающейся с премией. Заметим, что цена облигации, продающейся с дисконтом, при условии неизменной требуемой доходности растет. Обратный процесс происходит с ценой облигации, продающейся с премией. Цена обеих облигаций в момент погашения равняется номинальной стоимости.

Причины изменения цены облигации

Изменение цены облигации можно объяснить одной или несколькими из приведенных ниже причин.

1. Наблюдается изменение требуемой доходности, связанное с изменением кредитного качества эмитента.

2. Цена облигации, продающейся с премией или с дисконтом, меняется не под влиянием требуемой доходности, остающейся неизменной, а растет или падает по мере приближения даты погашения.

3. Наблюдается изменение требуемой доходности, связанное с изменением доходности сравнимых облигаций (т. е. изменение доходности, требуемое рынком).

Причины 2 и 3 подробно описаны в этой главе. Умение предсказать изменение кредитного качества эмитента (причина 1) до того, как это изменение будет признано рынком, — одна из важных составляющих успешного управления инвестициями.

СЛОЖНОСТИ ПРИ ОПРЕДЕЛЕНИИ ЦЕНЫ ОБЛИГАЦИИ

Описывая ценообразование облигаций, мы исходили из предположений о том, что:

1) следующая выплата купона состоится ровно через шесть месяцев;

2) денежные потоки известны;

3) соответствующая требуемая доходность может быть определена;

4) все денежные потоки дисконтируются по одной ставке.

Рассмотрим каждое из приведенных положений применительно к реальной практике.

Таблица 2.2. Данные о временно́м движении цены на 20-летнюю облигацию с купонной ставкой 10 %, продающуюся с дисконтом и с премией

Следующая выплата купона состоится раньше, чем через шесть месяцев

Если инвестор приобретает облигацию, купонная выплата по которой должна состояться раньше, чем через полгода, цена облигации может быть вычислена следующим образом:

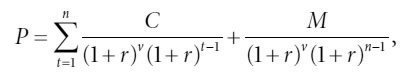
где:

Обратите внимание на то, что при v = 1 (т. е. в случае, когда следующая выплата купона состоится ровно через шесть месяцев) формула (2.9) сводится к формуле (2.6).

Денежные потоки могут быть неизвестны

Для облигаций без встроенного колл-опциона, эмитент которых не потерпел дефолта, денежные потоки известны. Между тем для большинства облигаций размер денежных потоков не может быть установлен с точностью. Причина — возможность отзыва облигаций эмитентом до наступления даты погашения. Для облигаций со встроенным колл-опционом денежный поток в первую очередь зависит от уровня текущих процентных ставок в сравнении с величиной купонной ставки. Так, эмитент, скорее всего, воспользуется своим правом на досрочное погашение облигаций, если процентные ставки упадут существенно ниже купонных и ему будет выгоднее выкупить облигационный выпуск, не дожидаясь даты погашения, а затем выпустить новые облигации с более низкой купонной ставкой. (Другой пример — ценные бумаги, обеспеченные ипотеками, подробно описанные в главах 11 и 12; индивидуальный заемщик имеет право предоплаты всех ипотечных обязательств или их части вне установленного графика.)

Таким образом, денежные потоки облигаций, которые могут быть выкуплены до даты погашения, зависят от текущих рыночных процентных ставок.

Выяснение соответствующей требуемой доходности

Для всех требуемых доходностей эталоном являются доходности, предлагаемые казначейскими ценными бумагами, речь о которых пойдет в главе 5. Аналитический принцип, которым мы руководствуемся в книге, — разложение требуемой доходности облигации на составляющие, описание которых читатель найдет в следующих главах.

Одна дисконтная ставка для всех денежных потоков

Анализируя ценообразование облигаций, мы до сих пор исходили из предположения о том, что все денежные потоки дисконтируются с помощью одной дисконтной ставки. В главе 5 мы покажем, что любая облигация может рассматриваться как пакет облигаций с нулевым купоном, причем в каждом случае для определения приведенной стоимости конкретного денежного потока должна использоваться особая дисконтная ставка.

ЦЕНООБРАЗОВАНИЕ ОБЛИГАЦИЙ С ПЛАВАЮЩЕЙ КУПОННОЙ СТАВКОЙ И ОБЛИГАЦИЙ С ОБРАТНОЙ ПЛАВАЮЩЕЙ КУПОННОЙ СТАВКОЙ

Ни для ценной бумаги с плавающей ставкой, ни для ценной бумаги с обратной плавающей ставкой денежный поток заранее неизвестен: он зависит от поведения референсной ставки в будущем.

Цена облигации с плавающей ставкой

Купонная ставка ценной бумаги с плавающей ставкой равна сумме референсной ставки и некоторого спреда или маржи. Купонная ставка облигации с плавающей ставкой может быть получена, например, при сложении ставки трехмесячного казначейского векселя (референсная ставка) и 50 базисных пунктов (спред).

Цена облигации с плавающей ставкой определяется двумя факторами: 1) величиной спреда и 2) ограничениями, которые могут быть наложены на перерасчет купона. Так, облигация с плавающей купонной ставкой может иметь максимальную купонную ставку, называемую верхней планкой (cap), или минимальную купонную ставку — нижнюю планку (floor). Цена облигации с плавающей ставкой будет приближаться к номинальной стоимости, если: 1) справедливый рыночный спред остается неизменным и 2) не достигается ни верхняя, ни нижняя планка^[9].

Если требуемый рыночный спред будет увеличиваться (уменьшаться), цена облигации будет опускаться ниже (подниматься выше) номинала. Если купонная ставка не будет равна сумме референсной ставки и спреда из-за ограничений, налагаемых верхней планкой, облигация с плавающей ставкой будет торговаться по цене более низкой, чем номинал.

Ценообразование облигации с обратной плавающей купонной ставкой

Как правило, облигация с обратной плавающей ставкой создается на основе ценной бумаги с фиксированной ставкой^[10].

Ценная бумага, с помощью которой создается облигация с обратной плавающей ставкой, носит название обеспечения. На основе обеспечения создаются две облигации: одна — с обычной плавающей купонной ставкой, другая — с обратной плавающей купонной ставкой. Процесс образования таких облигаций представлен на схеме внизу (рис. 2.2).

Две облигации создаются таким образом, что: 1) общая купонная выплата по обеим облигациям в каждый из периодов меньше или равна купонной выплате обеспечения в тот же период и 2) общая номинальная стоимость двух облигаций меньше или равна номинальной стоимости обеспечения. Облигация с плавающей ставкой и облигация с обратной плавающей ставкой должны быть структурированы таким образом, чтобы денежный поток, поступающий от обеспечения, был достаточен для удовлетворения обязательств по обеим ценным бумагам.

Рассмотрим 10-летнюю облигацию с купоном, выплачиваемым раз в полгода и равным 7,5 %. Допустим, что такие облигации в объеме $100 млн используются в качестве обеспечения для создания облигации с плавающей ставкой номинальной стоимостью $50 млн и облигации с обратной плавающей ставкой номинальной стоимостью $50 млн. Предположим, что купон пересчитывается каждые шесть месяцев в соответствии со следующей формулой:

купон облигации с плавающей ставкой = референсная ставка + 1 %; купон с обратной плавающей ставкой = 14 % — референсная ставка.

Напомним, что общая номинальная стоимость облигаций с обычной плавающей и обратной плавающей ставками равна номиналу обеспечения, т. е. $100 млн. Взвешенное среднее купонной ставки комбинации обеих облигаций равно:

0,5 × (референсная ставка + 1 %) + 0,5 × (14 % — референсная ставка) = 7,5 %.

Итак, вне зависимости от размера референсной ставки, комбинированная купонная ставка для двух облигаций равна купону обеспечения, т. е. 7,5 %.

Приведенная формула страдает одним недостатком. Предположим, что референсная ставка превышает 14 %. В этом случае результат, полученный при подсчете купона облигации с обратной плавающей ставкой, будет отрицательным числом. Чтобы этого не произошло, на купонную ставку облигации с обратной плавающей ставкой налагаются ограничения. Как правило, нижняя планка устанавливается на нуле. Существование такой нижней планки приводит к необходимости ограничения купона облигации с обычной плавающей ставкой, поскольку купонные выплаты по обеим облигациям не должны превышать процентные выплаты обеспечения. В нашей гипотетической структуре максимальной процентной ставкой облигации с плавающей ставкой может быть 15 %. Таким образом, при создании на основе обеспечения облигаций с плавающей и обратной плавающей ставками, для одной из них (облигации с обратной плавающей ставкой) существует нижняя планка, а для другой (с обычной плавающей ставкой) — верхняя.

Влияние верхней и нижней планки на ценообразование облигации пока нами не рассматривается. Для нас важно, что цена облигации с обратной плавающей ставкой определяется исходя из цены обеспечения и цены облигации с плавающей ставкой. Процесс можно записать в виде следующей формулы:

цена обеспечения = цена облигации с плавающей ставкой + цена облигации с обратной плавающей ставкой,

а значит:

цена облигации с обратной плавающей ставкой = цена обеспечения — цена облигации с плавающей ставкой.

Заметим, что референсная ставка влияет на цену облигации с обратной плавающей ставкой постольку, поскольку она ограничивает процентную ставку облигации с плавающей ставкой. Этот вывод чрезвычайно важен для нас. Некоторые инвесторы ошибочно полагают, что при росте купонной ставки цена облигации с обратной плавающей ставкой будет расти, если референсная ставка падает. Это неверно. Для ценообразования облигации с обратной плавающей ставкой существенно влияние процентных ставок на цену обеспечения. Референсная ставка имеет значение только в качестве фактора, ограничивающего купон облигации с плавающей ставкой.

ОБОЗНАЧЕНИЕ (КОТИРОВКА) ЦЕНЫ И НАКОПЛЕННЫЙ КУПОННЫЙ ДОХОД

Обозначение цены

В этой главе мы выбрали в качестве образца для анализа облигацию с номиналом, равным $1000. Очевидно, что облигация может иметь номинал более высокий или более низкий, нежели $1000. Соответственно, обозначая цену, трейдеры котируют ее как процент от номинала.

Облигация, продающаяся по номиналу, котируется по 100, т. е. ее цена составляет 100 % номинальной стоимости. Котировка облигации, торгующейся с дисконтом, обозначается числом меньше 100; облигация, которая торгуется с премией, котируется выше 100. В приведенной ниже таблице показано, каким образом котировка цены может быть переведена в цену в долларах.

Накопленный купонный доход

Инвестор, приобретающий облигацию в момент между датами выплат купона, должен компенсировать продавцу купонный доход, накопленный за время, прошедшее со дня последней выплаты купона до дня сделки^[11].

Эта сумма носит название накопленного купонного дохода. Вычисление накопленного купонного дохода проводится в зависимости от типа облигации. Для казначейских ценных бумаг (речь о них пойдет в главе 6) накопленный купонный доход рассчитывается исходя из реального числа дней, в течение которых продавец являлся держателем облигации. В случае корпоративных и муниципальных ценных бумаг вычисление накопленного купонного дохода ведется из расчета 360-дневного года и 30-дневного месяца.

Сумма, которую покупатель выплачивает продавцу, включает в себя как назначенную цену, так и накопленный купонный доход. Данная сумма часто называется полной ценой или грязной ценой. Цена облигации без учета накопленного купонного дохода носит название чистой цены.

Резюме

В этой главе мы рассмотрели, как установить цену облигации без встроенного колл-опциона. Цена такой облигации — это приведенная стоимость ее предполагаемых денежных потоков. Дисконтная ставка равняется доходности, предлагаемой сравнимыми облигациями на рынке. Для облигации без встроенного колл-опциона денежные потоки состоят из купонных выплат и номинальной стоимости, выплачиваемой в дату погашения. В случае облигации с нулевым купоном купонные выплаты отсутствуют. Цена, таким образом, будет равна приведенной стоимости номинала, причем число периодов, используемое для вычисления приведенной стоимости, — это удвоенное число лет, а дисконтная ставка — доходность за полгода.

Чем выше (ниже) требуемая доходность, тем ниже (выше) цена облигации. Очевидно, что цена облигации меняется в направлении, противоположном изменению требуемой доходности. Если купонная ставка равна требуемой доходности, облигация будет продаваться по номиналу. Если купонная ставка ниже (выше) требуемой доходности, облигация будет продаваться по цене более низкой (высокой), чем номинал; в этом случае говорят, что она торгуется с дисконтом (премией).

С течением времени цена облигации, торгующейся с премией или дисконтом, будет меняться, даже если требуемая доходность останется неизменной. При условии, что кредитное качество эмитента не меняется, ценовые изменения всякой облигации частично зависят от колебаний требуемой доходности, частично — от приближения даты погашения.

Цена облигации с плавающей купонной ставкой будет близка к номиналу, если требуемый рынком спред остается неизменным и на купонную ставку не налагаются ограничения. Цена облигации с обратной плавающей купонной ставкой зависит, во-первых, от цены обеспечения, на основе которого облигация была создана, и, во-вторых, от цены облигации с обычной плавающей ставкой.

Вопросы

1. Фондовый менеджер пенсионного фонда инвестирует $10 млн в долговое обязательство, которое в течение четырех лет должно приносить по 7,3 % ежегодно. Какова будущая стоимость этих $10 млн?

2. Предположим, что компания страхования жизни гарантировала пенсионному фонду выплату $14 млн через 4,5 года. Страховая компания получает от пенсионного фонда премию в размере $10,4 млн, которую может инвестировать на 4,5 года под годовой процент 6,25 %. Будут ли средства, полученные от данной инвестиции, достаточны для исполнения обязательства по выплате обещанных $14 млн?

3. а. Управляющий портфелем фонда, не подлежащего налогообложению, собирается инвестировать $500 000 в долговой инструмент, который в течение четырех лет будет выплачивать по 5,7 % годовых. По окончании четырехлетнего срока управляющий планирует реинвестировать полученные средства еще на три года и надеется, что в эти три года годовые процентные ставки для его инвестиции составят 7,2 %. Какова будущая стоимость данной инвестиции? b. Предположим, что управляющий портфелем из вопроса а получает возможность инвестировать свои $500 000 на семь лет в долговой инструмент, который раз в полгода должен выплачивать процентную ставку в 6,1 % годовых. Является ли эта инвестиция более выгодной, чем инвестиции из вопроса а?

4. Предположим, что управляющий портфелем приобретает восьмилетнюю облигацию с номиналом $10 млн и купоном 7 %, выплачиваемым раз в год. Первая выплата купона состоится через год. Какую сумму получит управляющий, если додержит облигацию до даты погашения и будет реинвестировать ежегодные купонные выплаты под годовой процент, равный 6,2 %?

5. а. Что происходит с ценой долгового обязательства, если дисконтная ставка, используемая для вычисления приведенной стоимости денежного потока облигации, растет? b. Пусть дисконтная ставка, используемая для вычисления приведенной стоимости денежного потока долгового обязательства, равна х %. Допустим, денежные потоки для данного долгового обязательства представляют собой $200 000 через четыре года и $200 000 через пять лет. Для какого из денежных потоков приведенная стоимость будет больше?

6. Обязательство корпоративного пенсионного фонда рассчитывается как приведенная стоимость будущих денежных выплат бенефициарам. Почему для проведения вычислений важно значение используемой для дисконтирования процентной ставки?

7. Управляющий пенсионным фондом знает, что у его фонда есть следующие обязательства по выплатам пенсий:

Предположим, что управляющий пенсионным фондом хочет инвестировать некую сумму денег, достаточную для исполнения обязательств фонда. Известно, что любая сумма денег, инвестированная в настоящий момент, может принести 7,6 % годовых. Сколько следует инвестировать сегодня, для того чтобы удовлетворить поток долговых обязательств?

8. Для каждой из облигаций вычислите цену номинальной стоимости, равной $1000, при условии купонных выплат, осуществляемых раз в полгода:

9. Рассмотрим облигацию, торгующуюся по номиналу $100 с купонной ставкой 6 % и сроком до погашения 10 лет.

а. Какова цена облигации, если требуемая доходность равна 15 %?

b. Какова цена облигации, если требуемая доходность с 15 % возросла до 16 %, и каково в этом случае процентное изменение цены?

с. Какова цена облигации, если требуемая доходность равна 5 %?

d. Какова цена облигации, если требуемая доходность возрастет с 5 % до 6 %, и каково в этом случае процентное изменение цены?

е. Проанализируйте результаты, полученные в пунктах b и d, и опишите волатильность цены облигации на рынке с высокими процентными ставками относительно ее волатильности на рынке, где процентные ставки низки.

10. Предположим, что три года назад вы приобрели долговое обязательство по номиналу в $100 000, причем срок до погашения составлял девять лет. Рыночная цена этого долгового обязательства в настоящее время равна $90 000. Назовите возможные причины падения цены, произошедшие в течение последних трех лет.

11. Вы просматриваете список цен облигаций и видите следующие значения цен (на $100 номинальной стоимости):

Вам кажется, что в таблице есть несколько ошибок. Не подсчитывая точное значение цены каждой облигации, скажите, цены каких облигаций указаны неверно и почему.

12. Что такое максимальная цена облигации?

13. Что такое «грязная» цена облигации?

14. Вы согласны со следующим утверждением: «Цена облигации с плавающей купонной ставкой всегда равна номинальной стоимости»? Обоснуйте свой ответ.

15. Вы согласны со следующим утверждением: «Цена облигации с обратной плавающей ставкой растет, если референсная ставка падает»? Обоснуйте свой ответ.

Примечания

7

Ценообразование облигаций со встроенными колл-опционами описано в главе 17.

8

В главе 4 вводится мера риска процентных ставок, известная как дюрация. Таким образом, сравнимыми мы будем в дальнейшем называть облигации с одинаковой дюрацией, а не сроком до погашения.

9

В промежутке между датами перерасчета купона облигация с обратной плавающей ставкой может торговаться ниже или выше номинала.

10

Облигация с обратной плавающей ставкой может также создаваться на основе свопа процентных ставок — в этом случае отпадает нужда в создании облигации с обычной плавающей ставкой.

11

Исключение составляют облигации, находящиеся в дефолте. Такие облигации котируются без учета накопленного купонного дохода.