Энциклопедия финансового риск-менеджмента

Алексей Лобанов, 2019

Эта книга – первое в России издание учебно-энциклопедического характера, в котором в соответствии с международными стандартами освещаются основные вопросы финансового риск-менеджмента. Издание дополнено новыми материалами по организационным аспектам риск-менеджмента, моделям эволюции процентных ставок, рискам страхования банковских вкладов и анализу макроэкономических рисков. Рассмотрены современные методы количественной оценки и управления финансовыми рисками, теория экстремальных значений, соглашения о форвардной процентной ставке и др. Дан систематизированный обзор методов количественного анализа, используемых в риск-менеджменте, моделей ценообразования и стратегий применения производных финансовых инструментов. Приведен обзор основных положений Нового базельского соглашения по капиталу 2004 г., выполненных на основе последней редакции соглашения от ноября 2006 г. Книга предназначена для профессионалов, непосредственно занимающихся оценкой и управлением рисками, преподавателей, студентов и аспирантов экономических факультетов вузов. Она также может использоваться для подготовки к сдаче международных экзаменов по финансовому риск-менеджменту на получение сертификатов Financial Risk Manager (FRM®) и Professional Risk Manager (PRM®).

II. Производные финансовые инструменты

В. Е. Барбаумов

2.1. Введение

В настоящее время для идентификации и измерения рисков широко используется теория производных финансовых инструментов. Изучение производных финансовых инструментов важно еще и потому, что сами эти инструменты являются источниками рисков как для различных финансовых институтов, так и для финансового рынка в целом. Кроме того, производные финансовые инструменты — одно из важнейших средств хеджирования тех или иных рисков. Именно поэтому данная глава посвящена изучению производных финансовых инструментов.

В главе рассматриваются как простейшие производные финансовые инструменты — форвардные и фьючерсные контракты, свопы, так и более сложные — опционы различных видов и инструменты со встроенными опционами. Основное внимание уделяется методам оценки таких инструментов и основным направлениям их использования.

Важнейшими производными финансовыми инструментами являются классические европейские и американские опционы. Подробно рассматриваются методы оценки таких опционов в случае, когда стоимость исходных активов определяется геометрическим броуновским движением. В частности, приводятся формулы Блэка-Шоулза для оценки европейских опционов и разбирается их использование. Применение классических опционов для хеджирования основных финансовых рисков также рассматривается в данной главе.

В заключительной части главы обосновывается построение биномиальной модели процентной ставки и ее использование для оценки финансовых инструментов, производных от процентных ставок: кэпов, флоров, свопционов и облигаций со встроенными опционами. Кроме того, приводится обзор и других моделей временной структуры процентных ставок.

2.2. Форвардные контракты и их основные характеристики

В настоящее время на развитых финансовых рынках важную роль играют так называемые производные инструменты (derivatives). Простейшим из производных инструментов является форвардный контракт.

Форвардный контракт, или форвард (forward), представляет собой соглашение купить или продать некоторые активы, называемые «базисными» (underlying), в определенный момент времени в будущем по заранее установленной цене. Обычно форвардные контракты заключаются между финансовым институтом и одним из его корпоративных клиентов. Таким образом, в форвардном контракте всегда присутствуют две стороны. При этом говорят, что сторона, согласившаяся в будущем купить активы, занимает длинную позицию, а сторона, согласившаяся продать активы, — короткую.

Так как стороны форвардного контракта равноправны и подвержены одному и тому же риску, то при заключении форвардного контракта никто никому ничего не платит. Это означает, что в момент заключения форвардного контракта стоимость его равна нулю.

Цену, по которой стороны согласились купить (и соответственно продать) активы, называют ценой поставки активов (delivery price). Цену поставки обозначим через K. Момент времени, когда происходит покупка и продажа активов, называют датой исполнения форвардного контракта, или датой поставки. Момент исполнения форвардного контракта обозначим через Т.

В момент исполнения форвардного контракта доход (выигрыш) от той или иной позиции определяется в зависимости от цены поставки K и спот-цены активов S_T. Доход от длинной позиции в момент Т равен S_T — K, а от короткой позиции K — S_T (рис. 2.1 и 2.2).

В дальнейшем мы будем исходить из следующих предположений:

1. Рынки являются совершенными (perfect):

• отсутствуют транзакционные расходы и налоги;

• ни один инвестор, покупая или продавая активы, не может повлиять на цены;

• разрешены короткие продажи.

2. Участники рынка могут неограниченно кредитовать или занимать деньги под одну и ту же безрисковую ставку (при непрерывном начислении).

3. По форвардным сделкам отсутствует кредитный риск.

4. Отсутствуют прибыльные арбитражные возможности, т. е. нельзя получить безрисковый доход за счет различия цен на активы.

При соблюдении этих условий все форвардные контракты на один и тот же вид активов с датой поставки Т будут в данный момент времени заключаться по одной и той же цене поставки.

Действительно, предположим, что в данный момент времени можно заключить форвардные контракты с ценами поставки К₁ и K₂, где K₁ > K₂.

Тогда можно занять короткую позицию по первому контракту и одновременно длинную позицию по второму контракту, при этом начальные затраты будут нулевыми. В момент Т исполнения контрактов будет получен доход K₁ — K₂ на каждую единицу активов. Так как отсутствуют прибыльные арбитражные возможности, то этого быть не может. В силу этого закона одной цены имеет смысл следующее определение:

Цена поставки, по которой в данный момент времени t заключаются форвардные контракты на данный вид активов с датой исполнения Т, называется форвардной ценой активов (forward price) на срок Т — t лет.

Итак, в начальный момент времени стоимость форвардного контракта равна нулю, так как в этот момент времени форвардная цена активов совпадает с ценой поставки этих активов. Однако через некоторое время форвардная цена активов может измениться, а цена поставки зафиксирована в контракте. Значит, после заключения форвардного контракта та или иная позиция по этому контракту может приобрести положительную или отрицательную стоимость. Эта величина показывает, что можно было бы получить, продав форвардный контракт, если бы существовал вторичный рынок для таких контрактов.

Если бы существовал вторичный рынок для форвардных контрактов, то стоимости длинной и короткой позиций в форвардном контракте определялись бы следующими равенствами:

где t — текущий момент времени (после заключения форвардного контракта);

Т — дата поставки;

K — цена поставки;

F — форвардная цена на момент t.

Докажем, например, равенство (2.1). Если

то займем сумму f_дл под безрисковую ставку на срок Т — 1 лет, приобретем длинную позицию по форвардному контракту с ценой поставки K и займем короткую позицию по контракту с ценой поставки F. В момент времени Т будет получен безрисковый доход:

При отсутствии прибыльных арбитражных возможностей этого быть не может. Предположим теперь, что

В этом случае произведем короткую продажу длинной позиции по форвардному контракту с ценой поставки K, полученную денежную сумму f_дл инвестируем под ставку на Т — t лет и займем длинную позицию по форвардному контракту с ценой поставки F. В момент времени Т доход составит:

Так как этот доход, очевидно, является безрисковым, то и неравенство (2.4) выполняться не может. Значит,

Популярным видом форвардных контрактов является соглашение о форвардной процентной ставке (forward rate agreement — FRA).

Соглашение о форвардной процентной ставке — это контракт, устанавливающий на определенный будущий период процентную ставку для заемщика и кредитора.

Сторона, занимающая длинную позицию по FRA, обязана через Т₁ месяцев от текущего момента взять кредит размером L на срок Т₂ — Т₁ месяцев под контрактную процентную ставку f_k. Сторона, занимающая короткую позицию по FRA, обязана через Т₁ месяцев от текущего момента предоставить кредит размером L на срок Т₂ — Т₁ месяцев под контрактную процентную ставку f_k.

Замечание. Обычно разность Т₂ — Т₁, измеряемая в месяцах, является делителем 12, причем если 12/(Т₂ — Т₁) = m, то контрактная процентная ставка определяется при начислении m раз в году.

Выигрыш стороны с длинной позицией по FRA на момент Т₂ составляет:

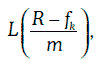
где R — рыночная процентная ставка на момент Т₁.

В самом деле, взяв кредит размером L под контрактную процентную ставку f_k, можно полученную сумму инвестировать под рыночную ставку R. Тогда выигрыш на момент Т составит:

Пример 2.1. Длинная позиция по FRA эквивалентна следующей стратегии:

• взять кредит за 5 месяцев;

• инвестировать полученную сумму на 2 месяца.

Во многих случаях по условиям FRA фактического размещения денежных средств не производится, а расчеты производятся в момент времени Т₁.

В этом случае сторона с длинной позицией по FRA в момент Т₁ получает денежную сумму а сторона с короткой позицией ее платит.

При отсутствии арбитражных возможностей контрактная процентная ставка по FRA должна совпадать с предполагаемой форвардной процентной ставкой _Т1f_Т2.

Для доказательства рассмотрим следующие две стратегии:

2.3. Форвардная цена финансовых активов

Форвардная цена активов зависит от вида этих активов и от того, приносят ли эти активы доходы. В данном разделе мы рассмотрим, как оцениваются форвардные цены финансовых активов, т. е. таких, которые рассматриваются участниками рынка только как средство инвестирования, в отличие от товаров, которые участники рынка рассматривают как средство потребления.

В зависимости от того, приносят ли данные финансовые активы доходы или нет, мы будем рассматривать три различных случая. В каждом из этих случаев предполагается, что соблюдаются предположения о рынке 1-4, изложенные выше.

2.3.1. Форвардная цена активов, не приносящих доходов

Такими активами, например, являются облигации с нулевыми купонами и акции, по которым не выплачиваются дивиденды.

Покажем, что форвардная цена F таких активов определяется равенством:

где S — спот-цена активов в текущий момент времени t;

— безрисковая процентная ставка при непрерывном начислении по инвестициям на Т — t лет;

Т — дата поставки активов.

При рассматриваемой стратегии не требуется производить начальных затрат, и эта стратегия не содержит риска.

По условию на рынке отсутствуют прибыльные арбитражные возможности.

то можно произвести короткую продажу базисных активов, полученную денежную сумму инвестировать под безрисковую ставку на Т — t лет и занять длинную позицию по форвардному контракту на эти активы.

Тогда в момент поставки активов будет получен безрисковый доход

что противоречит нашим предположениям о рынке. Следовательно,

Стоимости длинной и короткой позиций по форвардному контракту на активы, не приносящие доходов, определяются равенствами:

Пример 2.2. Найдем форвардную цену акции, не приносящей дивидендов, с поставкой через 3 месяца, если текущая цена акции 40 долл., а безрисковая процентная ставка на 3 месяца равна 3 %.

В данном случае

Тогда

Если на рынке форвардная цена акции оказалась равной 42 долл., то возможна следующая прибыльная арбитражная стратегия: занять 40 долл. на 3 месяца под безрисковую ставку 3 %, купить на спот-рынке акцию и занять короткую позицию по форвардному контракту. В момент поставки акции будет получен доход:

2.3.2. Форвардная цена активов, приносящих известные доходы

Такими активами могут служить купонные облигации или акции с известными заранее дивидендами.

Форвардная цена F активов с известными доходами определяется равенством:

где S — спот-цена активов в текущий момент времени t;

I — приведенное значение доходов, поступающих от активов за время от t до Т;

Т — дата поставки активов.

Стоимости длинной и короткой позиций по форвардному контракту на активы с известными доходами можно найти следующим образом:

Пример 2.3. Найдем форвардную цену акции с поставкой через 8 месяцев, по которой дивиденды в размере 5 долл. ожидаются через 2 и 5 месяцев, если текущая цена акции равна 100 долл., а безрисковые процентные ставки на 2, 5 и 8 месяцев соответственно равны 5, 5,5 и 6 % (при непрерывном начислении процентов).

В данном случае

2.3.3. Форвардная цена активов, обладающих постоянной дивидендной доходностью

Предположим, что доходы от активов выплачиваются в виде самих этих активов, причем так, что за время τ единица активов с учетом накопленных доходов превращается в единиц активов. В этом случае говорят, что активы обладают постоянной дивидендной доходностью при непрерывном начислении.

Иностранную валюту можно рассматривать как актив с постоянной дивидендной доходностью. В самом деле, единицу иностранной валюты можно инвестировать под безрисковую ставку в той стране, где действует эта валюта. Тогда через т лет единица иностранной валюты превратится в единиц этой валюты. Таким образом, иностранная валюта обладает постоянной дивидендной доходностью, и эта дивидендная доходность совпадает с безрисковой процентной ставкой .

Во многих случаях фондовые индексы также можно рассматривать как активы с постоянной дивидендной доходностью.

Форвардная цена F активов с постоянной дивидендной доходностью при непрерывном начислении может быть найдена по формуле:

В этом случае для стоимости длинной и короткой позиций по форвардному контракту имеем равенства:

Пример 2.4. Найдем 8-месячную форвардную цену английского фунта стерлингов, если текущий обменный курс равен 1,8 долл. за фунт, а безрисковые процентные ставки в США и в Англии при непрерывном начислении процентов равны 6 и 4 % соответственно.

2.4. Форвардная цена товаров

Пусть F — форвардная цена некоторого товара в момент времени t с датой поставки Т.

Покажем, что при отсутствии прибыльных арбитражных возможностей справедливо неравенство

Так как данная стратегия не требует никаких начальных затрат и не содержит риска, то это — прибыльная арбитражная стратегия. Следовательно,

Выясним теперь, существует ли прибыльная арбитражная стратегия, если

Для получения безрискового дохода необходимо произвести короткую продажу единицы товара. Однако, если этот товар большинством инвесторов используется для потребления или в производстве, сделать это без дополнительных затрат невозможно.

Если же товар в основном используется как средство инвестирования, то возможна следующая стратегия: произвести короткую продажу единицы товара, экономя при этом затраты на хранение товара, полученные средства инвестировать под безрисковую процентную ставку на Т — t лет и занять длинную позицию по форвардному контракту.

В момент Т будет получен доход

Таким образом, если товар используется в основном как средство инвестирования, а не потребления, то

Отметим, что к товарам, являющимся средством инвестирования, относятся, например, драгоценные металлы: золото, серебро, платина. Если же товар в основном используется как средство потребления, то

которое можно интерпретировать как меру физической полезности данного товара.

Пример 2.5. Найдем 10-месячную форвардную цену унции серебра, если текущая цена унции серебра равна 9 долл., затраты на хранение (охрану) составляют 0,24 долл. и выплачиваются поквартально вперед, а безрисковая процентная ставка для всех сроков при непрерывном начислении процентов составляет 10 %.

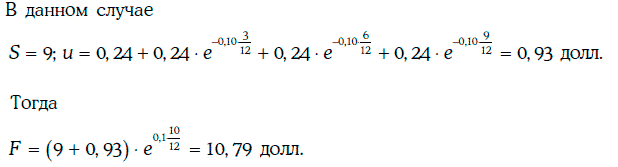
Пример 2.6. Оценим 9-месячную меру физической полезности одного барреля сырой нефти, если текущая цена барреля нефти равна 20,00 долл., затраты на хранение барреля нефти равны 0,5 долл. и оплачиваются в конце срока хранения, 9-месячная форвардная цена барреля нефти составляет 20,20 долл., а безрисковая процентная ставка на 9 месяцев при непрерывном начислении равна 8 %.

В данном случае

Значит, для определения физической полезности барреля нефти имеем уравнение:

Таким образом, 9-месячная мера физической полезности барреля сырой нефти составляет 9,77 %.

2.5. Фьючерсные контракты

Форвардные контракты, торговля которыми производится на специальных биржах, называют фьючерсными контрактами (fииге contfacts), или просто фьючерсами futures). Естественно, что для организации торговли форвардными контактами по бирже эти контракты должны быть стандартизированы по следующим параметрам:

• объему и качеству поставляемых активов;

• времени, месту и условиям поставки активов.

Еще одним важным отличием фьючерсных контрактов от форвардных является то, что биржа гарантирует исполнение всех фьючерсов, покупаемых или продаваемых на бирже. Для этого каждый форвардный контракт разбивается на два контракта:

• контракт между биржей и стороной, занимающей длинную позицию;

• контракт между биржей и стороной, занимающей короткую позицию.

В каждый момент времени длинная позиция биржи по любому форвардному контракту уравновешивается соответствующей короткой позицией. Таким образом, чистая фьючерсная позиция биржи в каждый момент времени равна нулю.

При такой организации торговли биржа берет на себя весь риск дефолта, так как, если одна из сторон не сможет выполнить свои обязательства по фьючерсному контракту, биржа все равно обязана исполнить другой контракт. Для уменьшения риска дефолта биржа требует, чтобы при открытии той или иной позиции вносилось специальное обеспечение.

При каждой фьючерсной бирже существует клиринговая палата. Все участники фьючерсного рынка должны иметь специальные счета в фирмах, являющихся членами клиринговой палаты. В момент открытия фьючерсной позиции на этот счет вносится специальное обеспечение, называемое начальной маржей (initial mafgin). Начальная маржа вносится либо наличными деньгами, либо высоколиквидными ценными бумагами, либо обеспечивается банковской гарантией. При этом начальная маржа составляет лишь малую долю от объема всего фьючерсного контракта, а счет маржи ежедневно корректируется. Эта процедура носит название переоценки фьючерсной позиции по рыночной стоимости (mavking to mafket — МТМ).

Для описания процедуры приведения фьючерсной позиции по рыночной стоимости предположим, что фьючерсная цена закрытия оказалась равной F₂, в то время как фьючерсная цена закрытия предыдущего дня была равна F₁.

Если F₂ < F₁, то счет маржи стороны, занимающей длинную позицию, дебетуется на величину A(F₂ — F₁), где А — объем контракта, и кредитуется счет маржи стороны, занимающей короткую позицию. Если же F₂ > F₁, то дебетуется счет маржи стороны с короткой позицией, а кредитуется счет маржи стороны с длинной позицией.

Если в конце дня сальдо счета маржи превысит размер начальной маржи, то инвестор имеет право снять излишек с этого счета и использовать его по своему усмотрению. Если же это сальдо окажется меньше размера начальной маржи, то возможны следующие два случая:

• сальдо счета маржи больше некоторой определенной величины, называемой маржей поддержки (maintenance margin);

• сальдо счета маржи меньше маржи поддержки.

В первом случае от инвестора не требуют дополнительного обеспечения. А во втором инвестор получает требование о внесении дополнительного обеспечения для того, чтобы сальдо счета маржи сравнялось с начальной маржей. Это дополнительное обеспечение называют вариационной маржей (variation margin). Обычно маржа поддержки составляет от 75 до 80 % начальной маржи.

Важнейшей особенностью организации фьючерсной торговли является то, что любая открытая позиция может быть закрыта в любой момент времени. Для этого достаточно занять противоположную позицию. При этом доход (убыток) стороны, занимающей длинную позицию, если по счету маржи не начисляются проценты, составит:

Аналогично доход (убыток) стороны, занимающей короткую позицию, будет равен:

Предположим, что в понедельник 1 марта 1999 г. открыта длинная позиция по казначейским облигациям США номиналом 100 000 долл. при фьючерсной цене Это означает, что при покупке казначейской облигации номиналом 100 000 долл. инвестор должен будет уплатить сумму, равную

Начальная маржа для данного контракта составляет 2500 долл., а маржа поддержки установлена в 2000 долл. Данная позиция сохраняется до пятницы 5 марта, а затем закрывается при цене открытия биржи в понедельник 8 марта. Будем считать, что по счету маржи проценты не начисляются и излишки не снимаются. В табл. 2.1 показано, как происходила переоценка фьючерсной позиции по рыночной стоимости. Как видите, убыток инвестора составляет 1062,50 долл.

C другой стороны, доход инвестора можно вычислить следующим образом:

Отметим еще несколько особенностей организации фьючерсной торговли на биржах.

1. Биржа устанавливает два вида ограничений:

• на размер чистой позиции инвестора по тем или иным активам. Цель состоит в снижении влияния одного инвестора на фьючерсный рынок;

• на величину дневного изменения фьючерсной цены. Если фьючерсная цена в течение одного дня изменяется на величину, превышающую установленный предел, торги останавливаются на определенное время. Цель установления таких пределов — ограничить размеры требований по марже.

2. В отличие от форвардных контрактов большая часть фьючерсных позиций закрывается до момента исполнения контрактов. Лишь очень небольшая доля контрактов заканчивается поставкой актива. Более того, много фьючерсных контрактов вообще не предполагают поставку активов, а по определенной схеме происходят денежные взаиморасчеты. Во многих случаях биржа требует специального уведомления, если инвестор будет настаивать на поставке активов.

2.6. Фьючерсные и форвардные цены активов

Для большего числа активов существует биржевой фьючерсный рынок. Но банки и другие финансовые институты предлагают различные виды форвардных сделок, т. е. существует еще и внебиржевой (over the counter — OTC) рынок форвардных контрактов. Таким образом, для одного и того же вида активов могут одновременно существовать две цены: форвардная и фьючерсная.

Однако если рынки удовлетворяют следующим условиям:

• отсутствуют транзакционные расходы и налоги;

• на форвардном и фьючерсном рынках инвесторы могут занимать длинные и короткие позиции на любое количество активов (хотя на биржевых рынках и существуют ограничения на чистые фьючерсные позиции);

• все инвесторы обладают достаточным капиталом (или кредитом), чтобы выполнить в случае необходимости все требования по марже;

• отсутствуют прибыльные арбитражные возможности;

• существует безрисковая процентная ставка, причем она одинакова для всех сроков и не меняется во времени, то форвардная и фьючерсная цены на один и тот же вид активов с одинаковыми датами поставки должны совпадать.

Именно вследствие этого утверждения во многих случаях при исследовании фьючерсных цен активов предполагается, что эти цены совпадают с соответствующими форвардными ценами.

Кроме того, при соблюдении вышеперечисленных условий имеет место следующее равенство:

Равенство (2.10) показывает, что фьючерсные цены активов в ряде случаев могут служить оценкой ожидаемой в будущем спот-цены этих активов. В частности, если активы положительно (отрицательно) коррелируют с рынком, то фьючерсная цена активов будет меньше (больше) ожидаемой спот-цены этих активов.

2.7. Спекулятивные стратегии на фьючерсных рынках

Всех участников фьючерсных рынков можно разделить на три категории: спекулянты, арбитражеры и хеджеры.

Спекулянтами (speculator) называют участников рынка, основная цель которых сводится к получению прибыли на основе прогнозирования будущих цен на рынке.

Арбитражерами (arbitrageur) считают тех участников рынка, которые получают безрисковую прибыль за счет временных рассогласований цен на различные виды активов.

Наконец, к хеджерам (hedger) относят тех, кто занимает определенные позиции по базисным активам и стремится застраховать свои позиции от неблагоприятных изменений цен на эти активы.

Обычно на биржах ведется торговля теми фьючерсными контрактами, к которым проявляют интерес все три категории участников рынка.

Рассмотрим вначале простейшие спекулятивные стратегии на фьючерсных рынках.

Предположим, что инвестор убежден в том, что между моментами времени t₁ и t₂ фьючерсная цена некоторых активов будет расти. В этом случае он в момент времени t₁ занимает длинную позицию по фьючерсному контракту на эти активы. Закрыв свою позицию в момент времени t₂, инвестор получит прибыль (убыток) в размере:

Таким образом, если оправдается прогноз инвестора о росте фьючерсной цены активов, то он получит прибыль. Однако если его прогноз окажется неверным, то он может понести и большие убытки.

С другой стороны, если инвестор считает, что между моментами времени t₁ и t₂ фьючерсная цена будет падать, то он может в момент времени t₁ занять короткую позицию по соответствующему фьючерсному контракту. Закрыв эту позицию в момент времени t₂, инвестор получит прибыль (убыток) в размере

Следовательно, если оправдается прогноз инвестора о падении фьючерсной цены, то он получит прибыль, в противном случае инвестор может понести большие убытки.

В целом, простейшие спекулятивные стратегии на фьючерсных рынках характеризуются высоким уровнем риска, но при благоприятных обстоятельствах могут обеспечить большую прибыль. По существу, эти стратегии эквивалентны аналогичным стратегиям на спот-рынках активов. Однако транзакционные расходы на фьючерсных рынках значительно ниже таких расходов на спот-рынках. Поэтому спекулятивные стратегии на фьючерсных рынках более привлекательны для инвесторов, чем аналогичные стратегии на спот-рынках.

Вторая группа спекулятивных стратегий на фьючерсных рынках опирается на прогноз поведения спреда (разницы) между фьючерсными ценами одних и тех же активов с различными датами поставок.

Предположим, что в данный момент времени t фьючерсные цены некоторых активов с датами поставок Т₁ и Т₂, Т₁ < Т₂ соответственно равны ^FT ^{(t) и F}T2 ^(t).

Если инвестор считает, что между моментами времени t₁ и t₂ межвременной спред будет возрастать, то он может в момент времени t₁ занять длинную позицию по долгосрочному фьючерсному контракту и короткую — по краткосрочному контракту. Закрыв свои позиции в момент времени t, инвестор получит прибыль (убыток) в размере:

Если же инвестор убежден, что между моментами времени t₁ и t₂ межвременной спред будет уменьшаться, то в момент времени t₁ он может занять короткую позицию по долгосрочному контракту и длинную — по краткосрочному фьючерсному контракту. Закрыв эти позиции в момент времени t₂, инвестор получит прибыль (убыток) в размере:

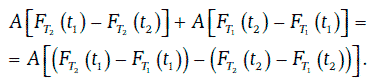
В обоих случаях, если оправдается прогноз инвестора о поведении межвременного спреда фьючерсных цен, он получит прибыль. Если же прогноз инвестора окажется неверным, то понесет убытки.

В целом стратегии, опирающиеся на межвременные спреды фьючерсных цен, являются менее рискованными, чем простейшие спекулятивные стратегии, и в то же время менее доходными.

Спекулятивные стратегии могут строиться и на основе прогнозирования отношения фьючерсных цен на различные виды активов.

Пусть F(t) и Ф(0 — фьючерсные цены в момент времени t на активы двух разных видов (и, вообще говоря, с разными датами поставок).

Если инвестор считает, что за время от момента t_I до момента t₂ отношение фьючерсных цен будет расти, то он может в момент времени t₁ занять длинную позицию по фьючерсным контрактам на активы первого вида и короткую позицию по фьючерсным контрактам на активы второго вида. При этом число фьючерсных контрактов N_: и N₂ инвестор должен выбрать так, чтобы соблюдалось следующее равенство:

Закрыв свои позиции в момент времени t₂, инвестор получит прибыль (убыток) в размере:

Аналогичным образом инвестор может применить спекулятивную стратегию, если он прогнозирует убывание отношения фьючерсных цен активов. В обоих случаях, если оправдается прогноз инвестора, он получит соответствующую прибыль.

Пример 2.7. Текущие фьючерсные цены американского доллара и немецкой марки — 30 и 16 руб. соответственно. Объемы имеющихся на рынке фьючерсных контрактов — 1000 долл. и 2000 марок. Инвестор, считающий, что отношение фьючерсных цен доллара и марки будет снижаться, занимает короткую позицию по 32 фьючерсам на доллары и длинную позицию по 30 фьючерсам на марки (в этом случае 32 • 1000 — 30 = 30 • 2000 — 16).

Если через месяц фьючерсные цены доллара и марки окажутся равными 29 и 15,50 руб. соответственно, то инвестор должен получить прибыль, так как

2.8. Фьючерсы на казначейские векселя.

Процентный арбитраж

Рассмотрим Т-летний фьючерсный контракт на казначейский вексель номиналом А, погашаемый через т лет после момента его поставки. Фьючерсную цену казначейского векселя в данный (нулевой) момент времени обозначим через F_T(τ).

Если данный фьючерсный контракт можно рассматривать как форвардный, то имеет место следующее равенство:

В самом деле, рассмотрим следующую стратегию:

Так как стратегия, очевидно, является безрисковой, то при отсутствии прибыльных арбитражных возможностей доход от стратегии должен быть нулевым, т. е.

Пример 2.8. Определим фьючерсную цену 90-дневного казначейского векселя номиналом 1 млн долл., когда до момента передачи остается 140 дней, а безрисковые процентные ставки (при непрерывном начислении) на 140 и 230 дней равны 8 и 8,25 % соответственно.

В данном случае

Замечание. Корпоративные клиенты финансовых институтов, владеющие рыночными ценными бумагами, могут получать краткосрочные кредиты под льготную процентную ставку, называемую ставкой репо (repo rate). Для этого корпорация продает ценные бумаги финансовому институту и одновременно заключает соглашение с ним о выкупе этих ценных бумаг. Так как такой кредит имеет хорошее обеспечение, то ставка по нему может быть снижена. Неявная же ставка репо — это, в сущности, такая ставка, под которую можно брать краткосрочный кредит с помощью фьючерсного рынка.

Неявная ставка репо позволяет выявить наличие прибыльных арбитражных возможностей и выбрать соответствующую стратегию.

Пример 2.9. Рыночная фьючерсная цена 90-дневного казначейского векселя номиналом 1 млн долл. с передачей через 56 дней равна 969 500 долл. Определим неявную ставку репо по кредитам на 56 дней, если безрисковая процентная ставка на 146 дней равна 12,27 %.

Предположим, что безрисковая процентная ставка на 56 дней равна 11 %. Тогда можно поступить следующим образом: занять 1 000 000 — е^{-0,1227 0,4} = 952 105 долл. на 56 дней под ставку 11 % и купить казначейский вексель номиналом 1 млн долл., погашаемый через 146 дней (его цена в точности равна 952 105 долл.), одновременно заняв короткую позицию по 56-дневному фьючерсному контракту на данный казначейский вексель. Через 56 дней будет получен арбитражный доход в размере:

2.9. Фьючерсные контракты на краткосрочные процентные ставки

Рассмотрим фьючерсный контракт на 3-месячную ставку LIBOR, который является одним из наиболее популярных фьючерсных контрактов на процентные ставки. Такой контракт можно интерпретировать следующим образом: сторона, занимающая короткую позицию, обязана в определенный будущий момент времени Т (дату поставки) разместить 1 млн долл. на евродолларовом депозите под установленную заранее трехмесячную ставку f (играющую роль цены поставки).

Рассмотренная выше ситуация эквивалентна той, когда сторона, занимающая короткую позицию, размещает в момент времени Т сумму 1 млн долл. под 3-месячную ставку LIBOR r, действующую в этот момент времени, а через три месяца после расчетной даты Т получает еще и компенсацию в размере Действительно, имеет место равенство:

Поэтому во фьючерсном контракте на 3-месячную ставку LIBOR не предполагается размещение средств на евродолларовых депозитах, а все расчеты производятся в наличной форме.

Через три месяца после расчетной даты Т сторона, занимающая короткую позицию, получает денежную сумму в размере а сторона, занимающая длинную позицию, ее платит.

Стандартные арбитражные рассуждения показывают, что форвардная 3-месячная ставка LIBOR должна удовлетворять следующему равенству:

2.10. Фьючерсные контракты на казначейские облигации

Фьючерсные контракты на казначейские облигации рассмотрим на примере фьючерсных контрактов на долгосрочные казначейские облигации США, торговля которыми ведется на Chicago Board of Trade (CBOT).

По условиям такого контракта производится передача любой казначейской облигации номиналом 100 000 долл., не погашаемой и не отзываемой в течение 15 лет после даты передачи.

После передачи облигации сторона, занимающая короткую позицию по фьючерсному контракту, получает денежную сумму в размере:

Конец ознакомительного фрагмента.